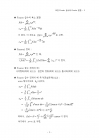Fourier_급수와_Fourier_변환
Fourier_급수와_Fourier_변환

Fourier_급수와_Fourier_변환

제 10 장 Fourier 급수와 Fourier 변환
목 차
1. 주기함수와 삼각 함수
2. Fourier 급수
3. Fourier 적분 변환
1. 주기 함수와 삼각 함수
★ 주기 함수의 정의 ;
위에서는 의 주기이다.
예)
★ 함수의 적분 공식 ;
☞
문서의 목차로
2. Fourier 급수
★ 함수 의 주기가 일 때,
로 쓸 수 있다. 이 때, 계수 은,
로 주어진다.
가 즉, 짝함수이면 이고
가 즉, 우함수이면 이다.
- 참고; 이 같은 전개가 가능하기 위해서는 가 영역에서 다음의 조건을 만족하여야 한다.
(1) 값에 대하여 단일 값을 가지며(single-valued), (2) 발산하지 않으며(bounded), (3) 유한한 개수의 최소치와 최대치를 가져야 하며, (4) 유한한 개수의 불연속점을 가져야 하며(불연속점 사이에서는 연속이어야 하며; piecewise continuous), 주기성 이 있어야 한다. 이 것을 Dirichlet의 조건이라고 한다.
★ Fourier 급수의 간단한 표현;
이 인 경우,
로 표현할 수 있으며, 계수는
으로 된다.
★ Fourier 급수의 복소 표현;
,
이 된다. 이 경우도 로 쓰면,
★ Parseval 정리 ;
인 때,
이 된다.
★ Fourier 급수 전개의 예 ;
사각형파(예제 10.2.1), 완전파 정류(예제 10.2.2), 톱니파(예제 10.2.3)
★ Fourier 급수 전개의 예 추가(연습문제10.2.2) ;
even 함수이므로 이다.
따라서, 이 된다.
여기에서 로 두면,
여기에서 로 정의되며 Riemann-zeta 함수라고 한다. (text의 378쪽 참조)
★ Gibbs 현상
....
목 차
1. 주기함수와 삼각 함수
2. Fourier 급수
3. Fourier 적분 변환
1. 주기 함수와 삼각 함수
★ 주기 함수의 정의 ;
위에서는 의 주기이다.
예)
★ 함수의 적분 공식 ;
☞
문서의 목차로
2. Fourier 급수
★ 함수 의 주기가 일 때,
로 쓸 수 있다. 이 때, 계수 은,
로 주어진다.
가 즉, 짝함수이면 이고
가 즉, 우함수이면 이다.
- 참고; 이 같은 전개가 가능하기 위해서는 가 영역에서 다음의 조건을 만족하여야 한다.
(1) 값에 대하여 단일 값을 가지며(single-valued), (2) 발산하지 않으며(bounded), (3) 유한한 개수의 최소치와 최대치를 가져야 하며, (4) 유한한 개수의 불연속점을 가져야 하며(불연속점 사이에서는 연속이어야 하며; piecewise continuous), 주기성 이 있어야 한다. 이 것을 Dirichlet의 조건이라고 한다.
★ Fourier 급수의 간단한 표현;
이 인 경우,
로 표현할 수 있으며, 계수는
으로 된다.
★ Fourier 급수의 복소 표현;
,
이 된다. 이 경우도 로 쓰면,
★ Parseval 정리 ;
인 때,
이 된다.
★ Fourier 급수 전개의 예 ;
사각형파(예제 10.2.1), 완전파 정류(예제 10.2.2), 톱니파(예제 10.2.3)
★ Fourier 급수 전개의 예 추가(연습문제10.2.2) ;
even 함수이므로 이다.
따라서, 이 된다.
여기에서 로 두면,
여기에서 로 정의되며 Riemann-zeta 함수라고 한다. (text의 378쪽 참조)
★ Gibbs 현상
....

-
 푸리에에 관한내용
푸리에에 관한내용
REPORT 학과 : 과목 : 분반 : 학번 : 성명 : 제출일자 : 목차 Fourier 급수 정의, 증명, 예시 Fourier 변환 정의, 증명, 예시 Fourier 적분 정의, 증명, 예시 Fourier급수와 변환 사이의 관계 및 차이점 Fo.. -
 푸리에변환에 대해
푸리에변환에 대해
푸리에 변환 주기신호의 주파수 성분 분석 ← 푸리에 급수 비주기신호의 주파수 성분 분석 ← 해석하고자 하는 신호의 성격 ⇒ 푸리에 급수(Fourier series) 푸리에 변환(Fourier transform) 이산시간 푸리에 변.. -
 Nyquists_Theorem과_Shannons_Theorem
Nyquists_Theorem과_Shannons_Theorem
Nyquist‘s Theorem과 Shannon's Theorem ■ Nyquist's Theorem Analog signal을 sampling하여 digital화 할때, 그 시점을 결정하는 sampling 주기는 원래 signal의 2배 이상이 되어야 한다는 것인데, 그것은 .. -
 dsp 05
dsp 05
제 5 장 이산 푸리에 변환 5.1 푸리에 급수 • 주기함수 • 기본 주파수(fundamental frequency) • 고조파(harmonics) ․ 주파수가 의 정수배인 정현파 ․ 제2 고조파, 제3 고조파, 제4 고조파,․․․ • 푸리에 급수(.. -
 퓨리에 변환[Fourier Transform]에 대해서
퓨리에 변환[Fourier Transform]에 대해서
Fourier Transform ■ 퓨리에 정리 - 모든 주기신호 및 비주기 신호는 기준주파수를 갖는 파형과 기준주파수의 정수배를 갖 는 파형들의 합으로 표현 할 수 있다. ■ 퓨리에 변환 - 비주기신호는 연속적인 무수.. -
 기초적인 신호분석과 전기량 측정을 위한 실험 기구의 사용 방법
기초적인 신호분석과 전기량 측정을 위한 실험 기구의 사용 방법
1.실험 목적 : 기초적인 신호분석과 전기량 측정을 위한 실험 기구의 사용 방법을 익혀본다. 2.기본 이론 1. 푸리에 급수 (Fourier Series) 임의의 주기함수를, 삼각함수로 구성되는 급수에 의하여 표현하는 .. -
 신호분석과 전기량 측정
신호분석과 전기량 측정
계측 및 신호처리 실험 보고서 [신호분석과 전기량 측정] 1. 실험제목 : 신호분석과 전기량 측정 2. 실험목적 Multi-meter, 함수발생기(Function Generator), 오실로스코프(Oscilloscope), LabVIEW 그리고 직.. -
 [현대 광학 실험] 푸리에광학-2F정렬
[현대 광학 실험] 푸리에광학-2F정렬
[현대 광학 실험] 푸리에광학-2F정렬 실험의 목적 광학 기기들의 사용방법과 그 특징들을 이해하여, 푸리에 변환 2f배열에 관하여 각각 다른 슬릿을 사용하여 어떻게 나타나게 되는지 알아보는 실험을 통하여 푸.. -
 d신호분석과 전기량 측정
d신호분석과 전기량 측정
1. 제 목 신호 분석과 전기량 측정 2. 목 적 함수발생기, 직류전압발생기, 오실로스코프, Multi-meter의 작동방법을 이해하고, 이들 실험기구를 이용해 신호를 분석하고 전기량을 측정한다. 3. 기본이론 1... -
 공학실험 랩뷰
공학실험 랩뷰
1.low pass filter에 대해서 조사하시오. ①연산증폭기에 대하여 저항(R)은 직렬로, 캐패시터(C)는 병렬로 연결하여 구성. ②가장 간단한 형태로 구현되어 모든 필터의 기본형으로 쓰임. ③주어진 차단 주파수 보..